多因素方差分析,用于研究一个因变量是否受到多个自变量(也称为因素)的影响,它检验多个因素取值水平的不同组合之间,因变量的均值之间是否存在显著的差异。多因素方差分析既可以分析单个因素的作用(主效应),也可以分析因素之间的交互作用(交互效应),还可以进行协方差分析,以及各个因素变量与协变量的交互作用。
根据观测变量(即因变量)的数目,可以把多因素方差分析分为:单变量多因素方差分析(也叫一元多因素方差分析)与多变量多因素方差分析(即多元多因素方差分析)。本文将重点讲述一元多因素方差分析,下篇文章将详细讲述多元多因素方差分析。
一元多因素方差分析:只有一个因变量,考察多个自变量对该因变量的影响。例如:分析不同品种、不同施肥量对农作物产量的影响时,可将农作物产量作为观测变量,品种和施肥量作为控制变量。利用多因素方差分析方法,研究不同品种、不同施肥量是如何影响农作物产量的,并进一步研究哪种品种与哪种水平的施肥量是提高农作物产量的最优组合。
一. 分析原理
通过计算F统计量,进行F检验。F统计量是平均组间平方和与平均组内平方和的比。

这里,把总的影响平方和记为SST,它分为两个部分,一部分是由控制变量引起的离差,记为SSA(组间离差平方和),另一部分是由随机变量引起的SSE(组内离差平方和)。即SST=SSA+SSE。
组间离差平方和SSA是各水平均值和总体均值离差的平方和,反映了控制变量的影响。组内离差平方和是每个数据与本水平组平均值离差的平方和,反映了数据抽样误差的大小程度。
通过F值看出,如果控制变量的不同水平对观测变量有显著影响,那观测变量的组间离差平方和就大,F值也大;相反,如果控制变量的不同水平没有对观测变量造成显著影响,那组内离差平方和就比较大,F值就比较小。
同时,SPSS还会依据F分布表给出相应的相伴概率值sig。如果sig小于显著性水平(一般显著性水平设为0.05、0.01、或者0.001),则认为控制变量不同水平下各总体均值有显著差异,反之,则不然。一般地,F值越大,则sig值越小。
二. SPSS分析案例
现在有一个公司员工的工资表,想看一下员工性别"gender"与接受教育年限"edu"这两个控制变量对员工"当前工资"的影响。采用多因素方差分析法,则要分别考虑"gender"、"edu"对"当前工资"的影响,称为主效应,还要考虑"gender*edu"对"当前工资"的影响,称为交互效应。
1. 分析步骤:将数据导入SPSS后,选择:分析—— 一般线性模型——单变量
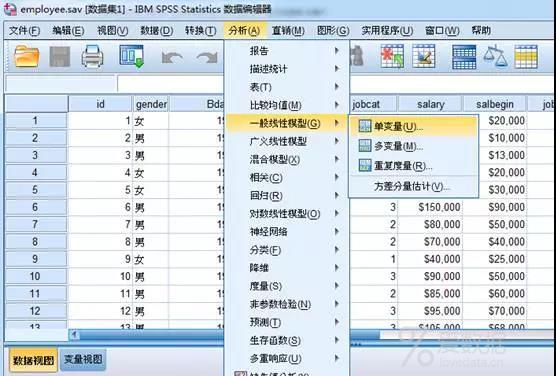
2. 将"当前工资"选入因变量(也就是观测变量),将性别"gender"与受教育年限"edu"选入固定因子(也就是控制变量)。

3. 选择"单变量"的"模型",打开对话框后选择"全因子",表示方差分析的模型包括所有因素的主效应,也包括因素之间的交互效应。然后"继续"。
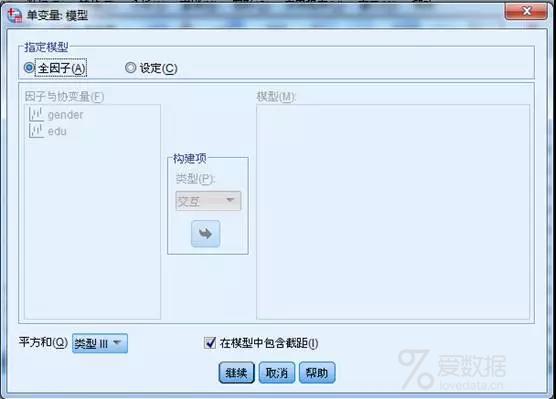
4. 打开"单变量"的"绘制"对话框,选择"gender"为横轴变量,选择"edu"为分线变量,单击"添加",即显示这两个因素变量的交互作用,即 "gender*edu"这个交互作用变量。
由于此例中"gender"只有两个水平,即男、女;而"edu"有多种水平。因此,如果主效应显著,则表明因素两种或多种水平之间存在显著性差异。事后可以继续对同一因素多个水平之间的均值差异进行比较,该过程称为多重比较。
但实际上如果主效应和交互效应都达到显著,我们更关心在多因素交互作用下,因变量有什么影响。
因此,如果交互效应显著的话,通常需要进行简单效应检验。所谓简单效应检验,是指一个因素的水平在另一个因素的 某个因素的某个水平上的变异。 例如我们本例中的, 如果gender与edu之间存在显著的交互作用, 我们可以检验当 gender为"女"时,edu的各个水平之间的差异,称为edu在"女"性水平上的简单效应;以及在"男"性水平上edu各水平之间的差异,称为edu在"男"性水平上的简单效应。
简单效应检验,实际上是把其中一个自变量固定在某一个特定的水平上,考察另一个自变量对因变量的影响。简单效应检验在SPSS里是用一个"MANOVA"命令来实现的。
同理,当我们检验三个自变量时,若这些自变量之间的交互作用显著,需要进行简单简单效应检验,即一个因素的水平在另外两个因素的水平结合上的效应。
也就是把两个因素固定在各自的某一个水平上,考察第三个因素对因变量的影响。也是用"MANOVA"命令来实现的。我们观察简单效应显著与否,是通过F值与sig值来看的,一般用sig值与我们设定的一个数值(0.05、0.01、或者0.001)来比较,若sig值大于该数值,说明简单效应不显著;反之,若sig值小于该数值,说明简单效应显著。
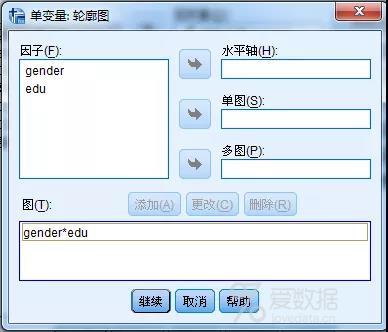
5. 打开"选项"对话框,将左边三个控制变量均移入右边,"显示均值",同时选中"描述统计",选中"比较主效应"。
6. 点击"确定"以后,就会在SPSS查看器里显示出结果。其中,最上面的那部分代码是我们所做的操作在SPSS里具体实现的步骤的代码。下面的表格是我们想要的结果,从表格里得出结论。
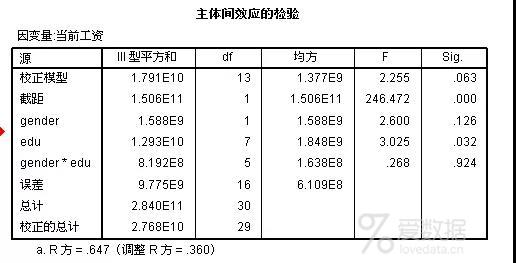
7. 从下面的"主体间效应的检验"表格里,我们比较性别gender、受教育程度edu、及gender*edu交互作用的F值及sig 值,看到 edu 的F值最大,sig 值最小,且 sig<0.05 。而 gender 与 gender*edu 的 sig 值都大于0.05,得出结论:"gender" 的主效应未达到显著,而"edu"的主效应达到显著,gender与edu的交互效应未达到显著(当交互效应达到显著时, 进而可以进行简单效应检验结果),就不需要进行简单效应检验。 则该公司员工"受教育程度"对员工"当前工资"的影响显著,而"性别"对"当前工资"的影响不明显。
8. 下图为均值分布图,即为两因素edu与gender作用下,因变量员工工资的均值分布情况。通常,若交互效应不显著时,图中的因素分布线均为平行线;若交互效应显著,图中的因素分线不平行。
此图中,将性别"gender"作为横轴变量,观察接受教育年限"edu"对因变量"当前工资"的影响。
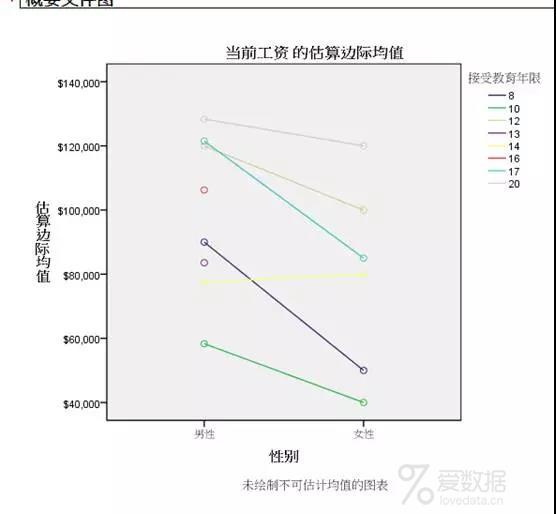
图中得出结论:当受教育年限为20年,一般为研究生水平的时候,男女工资差别不大;受教育年限为14年,一般为专科生水平,男女工资差别不明显。但当受教育年限为8年、10年、12年、17年的时候,男女工资差别较大,尤其为8年、17年的时候,男女工资差别尤其明显。
End.
来源:SPSS科研统计
- 我的微信公众号
- 微信扫一扫
-

- 我的微信公众号
- 微信扫一扫
-



评论