刻意练习15：用Minitab实现考虑交互的双因素方差分析

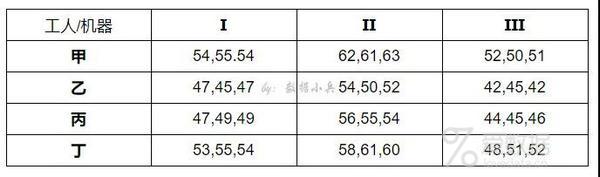
某工厂使用3种机型的机器生产同一款产品，现在老板想考察不同机型以及不同操作工人对产品的影响，为此他简单设计了一个小实验，让甲、乙、丙、丁四个工人操作机器Ⅰ、Ⅱ、Ⅲ各三天，其产品产量如下表所示，试分析工人和机器对产品产量是否有显著影响？

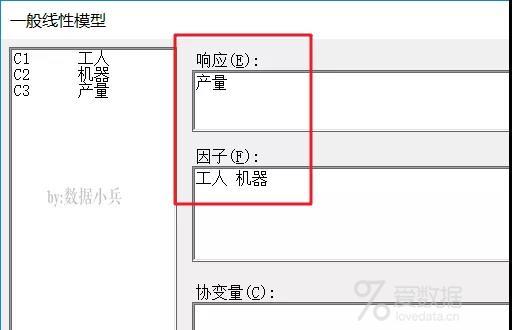
菜单：【分析】→【方差分析】→【一般线性模型】→【拟合一般线性模型】，minitab中的响应就是因变量，工人和机器作为因子。

打开【模型】对话框。在两个主效应的基础上，再添加二者的交互作用。

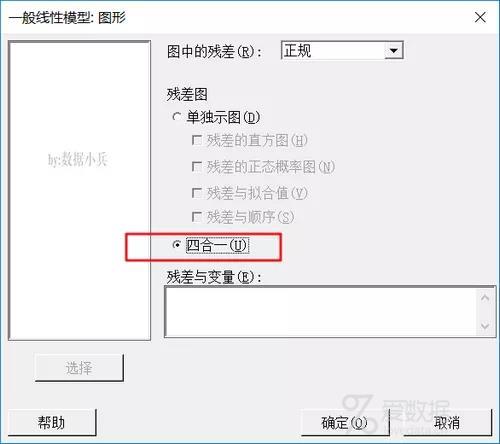
打开【图形】对话框。勾选【四合一】要求软件输出minitab特有的四合一残差诊断图形。

来看结果：

方差分析表。工人和机器两个主效应P<0.001，显著，有统计学意义，而二者的交互作用工人*机器P=0.819>0.05，说明交互作用不显著。（方差分析结果和SPSS一致）

再看一看残差是否近似正态分布，以及方差是否齐次。看残差四合一图形即可。

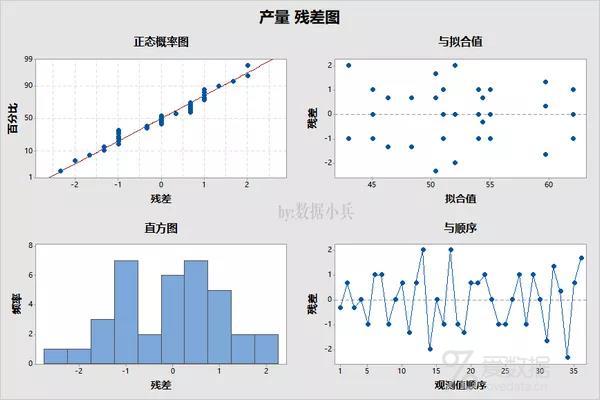
第1和第3幅图，可以看出数据正态性特征，第2幅图点的分布均匀无明显规律，能够说明方差齐次。基本满足方差分析前提条件。

接下来用效应图展示一下主效应和交互作用。

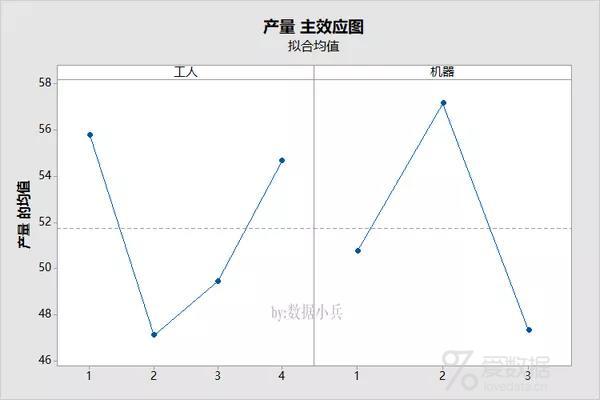
工人和机器两个因素对产量影响的主效应图。

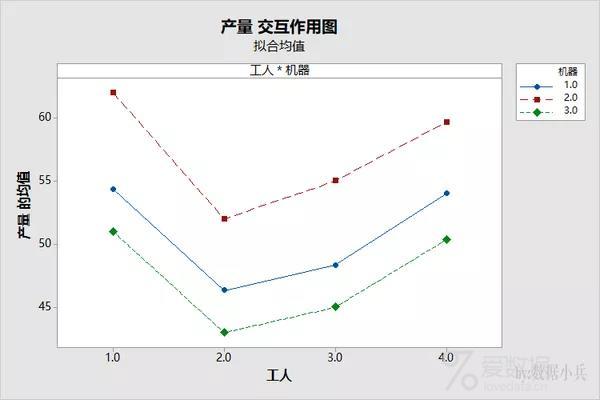
工人*机器交互作用对产量影响的交互作用图。无交叉也能说明交互作用不显著。

前面已经明确，工人和机器两个主效应显著，有统计学意义。那么就需要继续考察各水平之间的两两差异，此时需要进行两两比较。本例我们选择Bonferroni法。

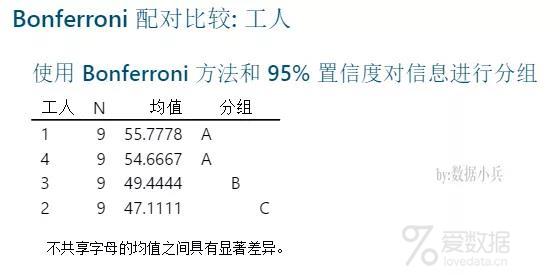
显然1/4工人和其他有显著差异，1和4之间无显著差异，且平均生产力突出。

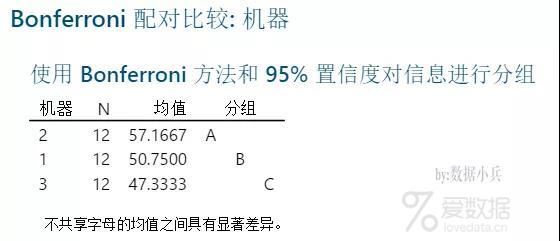
显然3个机器两两之间生产力差异显著，其中2号机器生产力最佳。

小结：

对方差分析的学习，入门阶段需要掌握单因素方差分析和双因素方差分析，具体还涉及基础假设条件的检定，以及多重比较方法的选择和解读。

此外，方差分析的学习离不开对试验设计的了解，三个以上因素的方差分析建议学习正交试验设计、响应面试验设计及其方差分析。

End.作者：数据小兵来源：博客本文均已和作者授权，如转载请与作者联系。