怎样理解时间序列二

在上一篇(怎样理解时间序列一)中介绍了一个简单的时间序列预测模型－指数平滑预测模型。说他简单是一点不假的，尤其是在和ARIMA模型对比之下。先看百科中对ARIM的介绍(下面截图来自百科)：

这一段介绍下来，放弃抵抗也是正常了，毕竟大部分人并非统计学出身，数学知识还能记住一半的也属另类，平时工作中用不到的知识忘了也就忘了。可是在企业中突然被老板叫去做预测怎么办呢？下面我尽量用人话来介绍一下ARIMA模型，不打算写太多的公式了，很累的。

理解了一个模型的参数，就可以填入适合的参数值，那么这个模型也就可以用了。所以这一篇就重点介绍这个模型各参数的意义。首先看下ARIMA完整的模型表达式： (s为周期步长)，需要我们理解的参数都在这了。

首先，我先概述一下，单纯的讲ARIMA模型是不行的，它和其他几个模型有着千丝万缕的关系，首先是AR(p)模型，然后是MA(q)模型，AR(p)模型和MA(q)模型可以组合成ARMA(p,q)模型，如果序列需要做一下差分，就成了ARIMA(p,d,q)模型，如果原序列有季节性呢，就有了周期s，如果原序列的周期性和长期趋势、随机波动之间有着复杂的交互影响，那么就要使用乘法季节模型，就是 了。

上一篇有说道，ARIMA模型的预测原理是分析序列自身，提取序列中所有相关性的信息来拟合函数，并用该函数进行预测。预测的准或不准，都在于这个函数拟合的好不好。AR(p)模型，全称是p阶回归模型；MA(q)模型，全称是q阶移动平均模型；ARMA模型，全称是自回归移动平均模型。这三个模型都有自己的函数公式，这三个公式可以画成不同的曲线，如果它们所画出来的曲线和历史序列非常相似，那么恭喜你，已经找到很好的拟合函数了，后面就可以用这个函数来进行预测了。我们还是看一下这三个公式(限制条件就不写了)：

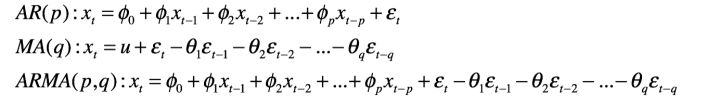
公式看不看无所谓，主要是想说从公式中可以看出这几个信息：

1. ARMA(p,q)模型的统计性质就是AR(p)模型和MA(q)模型的有机组合，如果q＝0，它就退化成了AR(p)模型，如果p＝0，就退化成了MA(q)模型。
2. p和q不同，模型的阶数不同，未知参数不同(这个参数的问题后面再说)，拟合出来的曲线不同。

到这里大家应该看得出来，p和q的性质了，定义不同的p和q可以拟合出不同的曲线，如果这个曲线和原序列拟合度很高，那就可以用来预测了。还有其他参数没有介绍，那么一定是因为并非所有的序列都可以通过ARMA拟合出来的，有些序列仅仅调整p和q的值是不能拟合出来的，因为ARMA模型要求序列一定是平稳的。

这里有了一个新的概念，就是平稳性，那么怎么来理解平稳性，它的一种表达是序列的统计性质不随时间的推移而发生变化。这也是可以理解的，我费了老大的功夫把函数拟合出来，结果时间变了我的函数就不对了，还怎么玩下去？可是那些不是平稳的序列要怎样预测呢，生活中大量的数据都不是平稳的，有趋势的不平稳，有周期的也不平稳，没有趋势没有周期序列本就少了很多，而且它们的也还不一定平稳呢。为了能够预测不平稳的序列，采用了一个方法叫做差分，就这样ARIMA模型出现了，参数d也可以现身了。

ARIMA模型中参数d就是用作差分的，d=1就是做1阶差分，d=2就是2阶差分。什么是差分？我这里就写一个一阶差分的公式简单表达下，更多的就百度查概念吧。

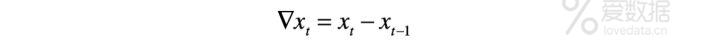
了解差分之后，我们继续讲，一个不平稳的序列，我们可以做1阶差分，也可以做多阶差分，还可以做步长大于1的差分，这么多选择，怎样才能最合适的让序列平稳，而且避免过差分呢(每次差分都会带来信息的损失，因此差分要点到为止，平稳后再差分虽然也平稳但是信息就没了)？一般来说，序列蕴含显著的线性趋势，1阶差分就可以实现序列平稳；序列如果是曲线趋势，2阶或3阶也差不多可以平稳了；如果序列有周期因素，那么进行步长为周期长度的差分运算，可以提取周期信息。

这里就带来了一个问题，进行差分运算后，序列到底是不是平稳的？除了上文我说的有趋势的不平稳、有周期的不平稳之外，衡量一个序列是否平稳，有两个重要的统计性质：

• 均值为常数：也就是不论哪一个时间范围，取它的期望值都是一样的
• 自协方差函数和自相关系数只依赖于时间的平移长度而与时间的起止点无关

了解它的统计性质之后，验证一个序列是否平稳，到底要怎样判断？常用的两个方法，首先，用眼睛看，有些不平稳一眼就看出来干嘛还动手呢？肉眼已经看不出来的，使用自相关图检验，平稳序列具有短期相关性。如下图(来源百度图片，侵删)第一个就不平稳，延迟阶数很高却依然有自相关性，第二个图就是平稳的了，延迟2阶之后的自相关系数都在两杯标准差范围内了。

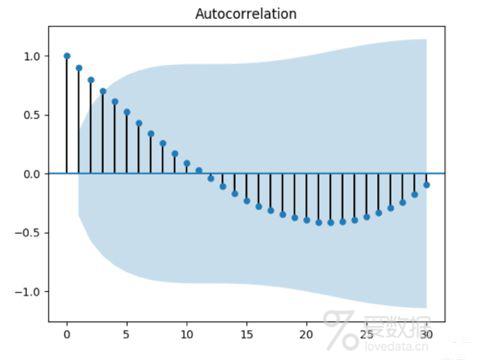
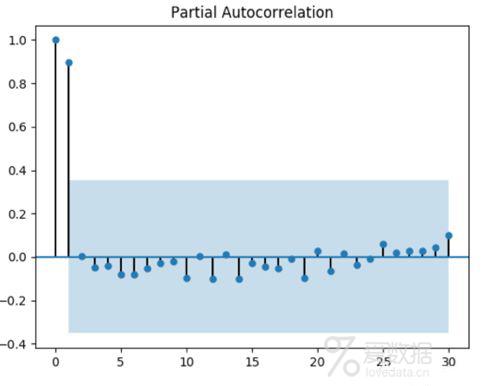
这样，我们通过差分让一个序列平稳了之后，就可以继续用ARMA模型来拟合了。前文说了用ARMA(p,q)可以拟合出不同的曲线，还有个问题没有讲，一条平稳的曲线放在这里，要怎样才能拟合出合适的函数来呢？这中间要有两部，首先是模型的定阶，也就是p为多少，q为多少；其次，通过最上面ARMA(p,q)的公式可以看出来，这个模型中含有p＋q＋2个未知参数，这些未知参数怎么计算出来。

首先是模型的定阶，也就是确定p和q这两个参数，一般是通过序列的自相关系数和偏自相关系数来进行判断，如下表所示：

这里有两个概念需要补充一下了，什么叫做拖尾，什么叫做截尾。这个是用自相关系数图(偏自相关系数图)来看，如果自相关系数(或偏自相关系数)在p(或q)阶之后断崖式下跌，和p(或q)阶之前差距很大，那么就是p(或q)阶截尾了，如果自相关系数(或偏自相关系数)拖拖拉拉的没有这种干脆爽快的下跌，那么就是拖尾。从我的描述中也可以看出来，判断截尾或拖尾有一定的主观因素，毕竟不是所有的自相关图都可以截尾的那么清晰。因此确定模型的阶数还需要有一定的经验因素在其中。

在确定了模型的阶数之后，就需要评估模型参数了，从前面公式中可以看出来，无论是AR(p)模型、MA(q)模型还是ARMA(p,q)模型都有一堆的参数，这要是一个一个找出来要累死。这样参数估计有点麻烦，方法有矩估计、最大似然估计和最小二乘估计，其中矩估计精度不高，常用的是最大释然估计和最小二乘估计。这些方法具体的过程讲道理我也没有看懂，不过幸运的是这些过程不需要我们自己做，有统计软件在，这些参数可以交给它们了。

到现在为止，不平稳的序列搞平稳了，平稳后的序列找出了模型，模型中的参数也识别出来了，最终拟合出来的函数应该出来了吧？函数是出来了，这个不是问题，可问题是，这个函数靠谱么？那么又引来了一个新的问题，就是模型的检验，通过验证的模型才是可用的模型。模型要怎样验证的，需要另一个新的概念叫做残差，残差什么样才算通过验证呢？残差序列是白噪声序列的就可以通过了，为什么是这样呢？如果序列一开始就是白噪声怎么办？如果拟合没有通过检验怎么办？有哪些序列需要其他的参数才能拟合？这一段中所有的问题，留在下一篇在讲吧。

End.

作者：jiago 王佳东fr来源：知乎

本文均已和作者授权，如转载请与作者联系。