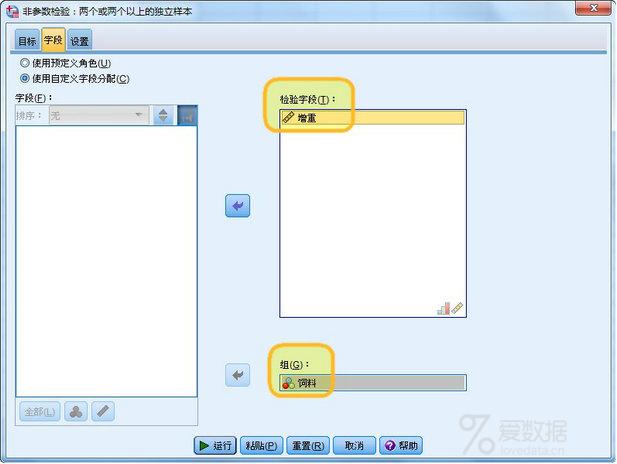
3组以上数据均值有无差异,通常我们使用单因素方差分析来完成,前提是3组数据分别来自正态分布总体,且方差齐次,对于正态分布来说,可以不用过于严苛,只要数据近似服从正态分布即可,至少不要出现太过严重的偏态就可以继续使用单因素方差分析。 已经有成熟的研究经验,方差分析对正态分布的要求有一定耐性,并不过分敏感,(微小偏态)近似正态分布的数据继续采取ANOVA单因素方差分析是可以的,结果仍然可靠。 遇到偏态严重的数据怎么办呢?此时可以尝试非参数检验方法:Kruskal-Wallis 单因素 ANOVA(k 个样本)检验。 现在我们收集到4种不同饲料增肥效果的实验数据,假设4组数据严重偏离正态分布,请使用Kruskal-Wallis非参数方法检验饲料效果的差异性。 菜单【分析】→【非参数检验】→【独立样本】, 部分参数设置:




来看结果: 在输出的统计表格上双击激活编辑器,进入模型查看器窗口。

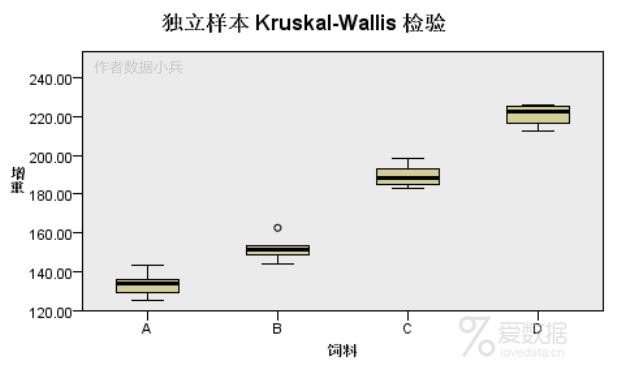
Kruskal-Wallis检验的原假设:假设不同饲料增肥效果无差异。 Kruskal-Wallis检验的p值=0.001<0.05,说明原假设不成立,表明不同饲料的增肥效果差异显著。 不同饲料增肥效果的平均值,图形可视化效果如下:

既然不同饲料效果有差异,而且差异显著,那么我们就希望进一步获知到底哪一个饲料才是最佳的。此时需要多重比较方法,Kruskal-Wallis检验可以输出相应的结果。

来看多重比较的结果:

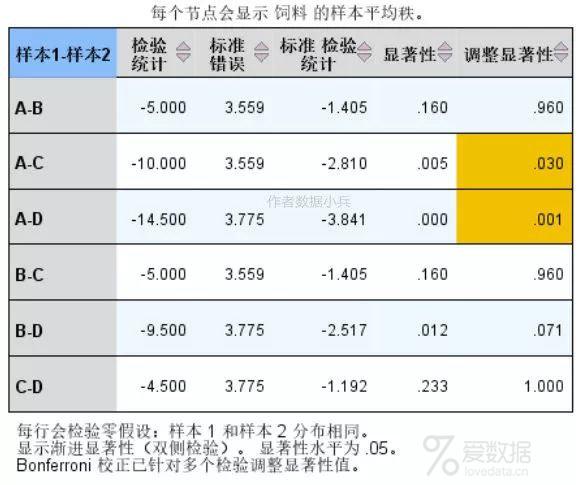
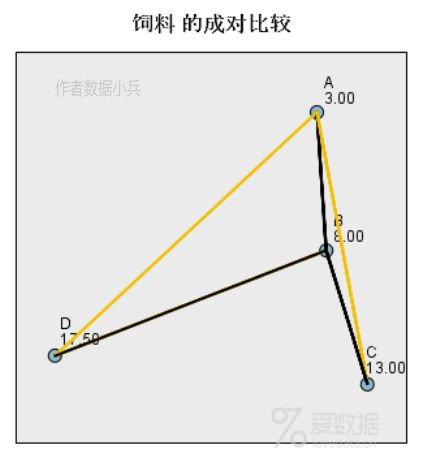
多重比较原假设:两组数据间差异。 大家看表格的最后一列调整后的显著性p值,A-C,A-D差异检验的p值<0.05,说明原假设不成立,即表明A和C、D的差异显著。其他两两之间的差异不显著。还有一点发现:D饲料的平均增肥效果最大,C次之,A最小。 多重比较的可视化效果如下:

黄色线条对应的水平之间差异显著,黑色线条对应的水平之间差异不显著。结合前面不同饲料增肥效果的箱线图,再结合方差分析的结果,我们可以得到如下结论:不同饲料的增肥效果有明显差异,相比较而言,D饲料效果最佳,C饲料次之。
End.作者:数据小兵来源:博客本文均已和作者授权,如转载请与作者联系。
- 我的微信公众号
- 微信扫一扫
-

- 我的微信公众号
- 微信扫一扫
-



评论