排序算法-选择排序

首先分享一张堆排序的动态图，来自Wikipedia.

接下来继续回顾下各个排序算法的时间复杂度和空间复杂度的表格：

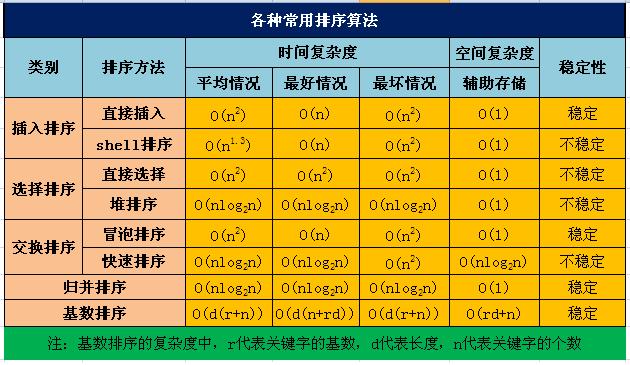
一、直接选择排序

原理：每轮比较之后都会记录最大值的下标，最后将该位置的元素与当前最后一个元素交换。

1. //传入的n是数组长度
2. void choiceSort(intnums[],intn){
3. for(inti =n-1; i >=0; --i){
4. intt= i;
5. for(intj =0; j < i; j++){
6. if(nums[j] > nums[t]){
7. t= j;
8. }
9. }
10. swap(nums[i], nums[t]);
11. }
12. }

二、堆排序（大根堆）

思想：需要建立大根堆。首先初始化大根堆，然后将堆顶元素和最后一个元素交换；接着使用剩下的n-1个元素重新建立大根堆，然后又将堆顶元素与第n-1个元素交换，依次循环，直到剩下最后一个元素为止。对的存储，使用数组，需要注意：

1.如果数组下标从0开始，则第i个节点的左孩子是2 * i +1，右孩子是2* i + 2;

2.如果数组下标从1开始，则第i个节点的左孩子是2 * i，右孩子是2* i +１.

首先需要建立一个堆调整函数。

1. //7.堆排序（大根堆）[数组下标从0开始],m表示起始下标，n表示终止数字的下标
2. voidHeapAdjust(intnums[],intj,intn){
3. intvalue= nums[j];
4. inti =2* j +1;
5. while(i <= n){
6. //left孩子为2i+1,right孩子为2i+2
7. if(i < n && nums[i] < nums[i+1]){//找到孩子中较大的那个下标
8. ++i;
9. }
10. if(value> nums[i]){//左右孩子中获胜者与父亲的比较
11. break;
12. }
13. //将孩子结点上位，则以孩子结点的位置进行下一轮的筛选
14. nums[j]= nums[i];
15. j = i;
16. i =2* i +1;//因为下标是零开始，所以左孩子这里是2*i+1
17. }
18. nums[j]=value;//插入最开始不和谐的元素
19. }

1. //堆排序
2. voidHeapSort(int*nums,intn){
3. inti;
4. //初始化大根堆
5. for(inti = n/2; i >=0; i--){
6. HeapAdjust(nums, i, n-1);//注意，下标从0开始，所以是n-1
7. }
8. for(i = n-1; i >=0; i--){
9. //cout<<nums[0]<<" "<<endl;
10. swap(nums[0], nums[i]);//交换堆顶和最后一个元素，即每次将剩余元素中的最大者放到最后面
11. HeapAdjust(nums,0, i-1);//重新调整堆顶节点成为大顶堆
12. }
13. }

三、测试

下面简单的测试下堆排序：

1. #include<iostream>
2. usingnamespacestd;
3. voidchoiceSort(intnums[],intn);
4. voidHeapSort(int*a,intlen);
5. voidprint_array(intnums[],intn);
6. intmain()
7. {
8. intnums[]={2,5,4,3,7,6,9,21,22,121,10,8,1};//quikSort(nums,0,sizeof(nums)/sizeof(nums[0])-1);
9. intn =sizeof(nums)/sizeof(nums[0]);
10. //choiceSort(nums, n);
11. HeapSort(nums,0, n-1);
12. print_array(nums, n);
13. return0;
14. }
16. //将遍历数组写在了一个函数里，方便调用
17. voidprint_array(intnums[],intn){
18. for(inti =0; i<n; i++){
19. cout<<nums[i]<<" ";
20. }
21. cout<<endl;
22. }

输出结果：

1 2 3 4 5 6 7 8 9 10 21 22 121

Process returned 0 (0x0) execution time : 0.083 s

Press any key to continue.

End.

作者：拾毅者

来源：『刘帝伟』维护的个人技术博客

本文均已和作者授权，如转载请与作者联系。