搭建数学模型的小技巧

在职业经历中，听过不同的角色提到"建模"二字，观察最终结果，发现不同角色提到的建模含义是不同的：

• 产品/运营团队的"建模"：业务模型，某一个项目的业务闭环，在PM团队称模型。
• 分析建模：满满的德尔菲法[1]，将一个大问题拆解成几个模块，每个模块中的指标请专家赋权，像多元一次方程似的，将指标值套进xyz中，得到一个模块的指数，再将模块赋值，得到综合指数。

大致如下：

Index=a*index1+b*index2+c*index3

Index1=m1*x1+m2*x2+m3*x3

Index2=n1*y1+n2*y2+n3*y3

Index3=k1*z1+k2*z2+k3*z3+k4*z4

这种方法存在的问题：

• 量纲问题，量纲不同，直接处理会受量纲大小影响，量纲单位越大，影响越大
• 把指标间的关系当做线性关系，但实质上大部分指标非线性关系，指标在不同阶段对结果的影响度是变化的。
• 数学建模：业务思考逻辑的量化。是对上一类的优化，不论赋权方式与处理指标的方式都体现了对业务的理解和基于数学的量化结合。经过多个项目实践，这类算法对于数据驱动业务来说最有效。推测原因：
• 业务视角 甚至比业务视角更深层次，因为有大量数据的规律总结与业务视角结合。
• 准确与召回率高于业务自用的分析建模方法，且数学处理方式对业务方是透明的，能懂，敢用。
• 统计建模：现有常用的多元统计模型。使用各种统计工具都可以实现的多元统计建模。
• 优势："傻瓜软件"不需要知道模型的数学推导过程，会用就可以使用。
• 劣势：因为是现成写好的模型与参数，使建模效果不佳，更适合课堂教学，实践中数据要复杂的多，效果也不理想（各种检验通不过）。
• 机器学习：推荐系统，AI都是机器学习，但要真正用好，需要懂模型的推导过程，以及调参之道，否则分析出来可能是错误的结论，而业务会因为模型本身是黑盒，准确率欠佳而弃用。在职业经历中，未见到过用户建模/内容建模用于分析，然后通过分析驱动业务的成功案例，我仍需继续修炼。

本篇重点给大家推介数学建模的一些小技巧。

分析师建模的业务场景一般是两种大场景，多个小场景，按大场景去建模，对模型小迭代，应用于大场景。

• 场景1：用户分层运营或管理

不论是C端产品，还是B端产品，任何一个产品都有用户或客户，在海量数据面前，需要一套方法对用户进行科学分层。这里可能有人提RFM，该模型切分的太生硬，准确率不高。

• 场景2：做指数。

衡量健康度或排名，需要产出指数用于排名。尤其在复杂的业务中，借助指数看问题，有助于我们将问题降维，减小信息熵，更容易发现管理可驱动的关键靶子。

函数照进现实

指标的用法取决于：你对其所衡量业务的理解

• 线性

即：y=a*x 一元一次线性方程

现实中业务比较复杂，结果会受多因素影响，若只靠单因素建模，不会被取信的。

• 多元一次

即：y=ax+by+c 多元一次方程

上文中分析建模便是这个思路，实际业务中影响因变量y的，随着是空扩展，是变化的，该模型忽略了这些变化，但因为容易实现，比较受PM童鞋自己建模的欢迎。但请注意：效果准确度很差。

• 对数函数

公式如图：（a称为底数，x是你的指标）

观察对数函数曲线的形态（a>1时较常用），特征：随着x的变大，y值逐渐变小

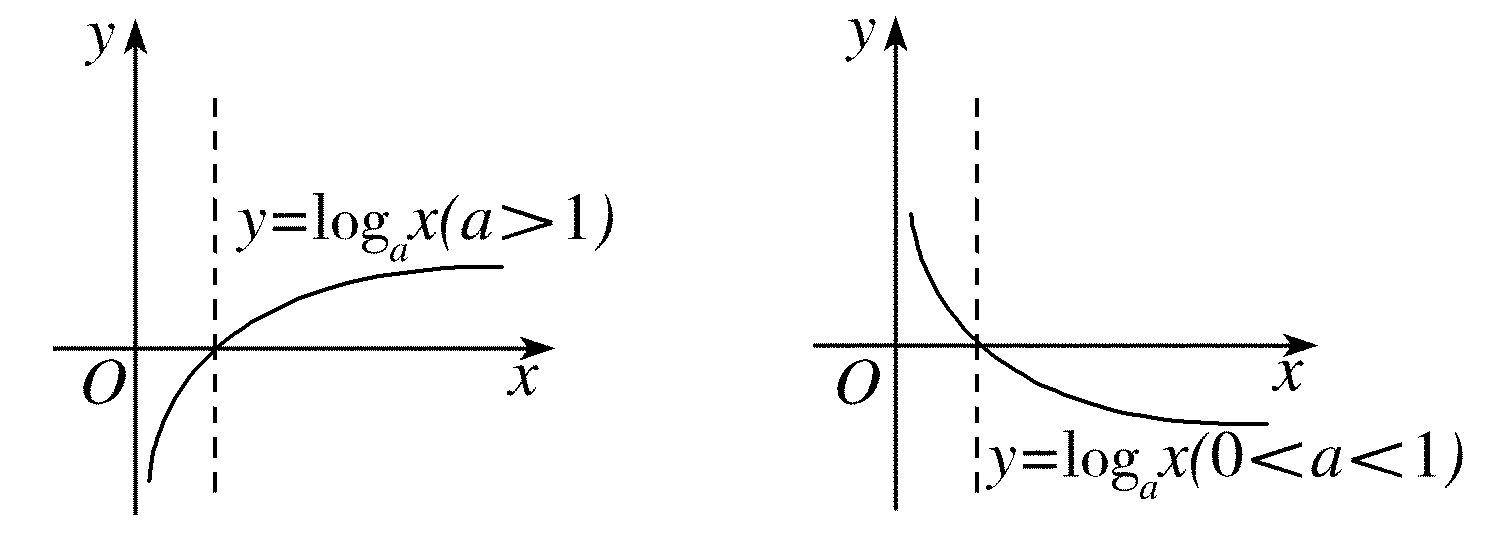
照进现实

对y的影响边际递减：若你的指标形态近似一条直线，而该指标对你的目标的影响应是边际递减的，那么，可以对该指标取对数，用作建模。举例：目标是计算活跃度指数，发帖数是其中一个影响因素，衡量活跃度时，并不是发帖数无限度地越高越好，而是在起初发帖增加时，对活跃度的边际贡献较大，而在达到一定的水平后，再增加发帖，对其活跃度而言就不那么重要了，即边际贡献应该减少。形态正如上述对数函数。在现实业务分析中，这样的指标非常多。

注意事项：底数a大于1时，当x小于1时，为负，若你的指标有0~1之间的数，为了保证是正值，往往函数演变成log(x+1)，用的较多的是ln(x+1）--excel有此函数。

• 指数函数

公式如图：x是你的指标，a是个常数，可自定义

观察指数函数曲线的形态（a大于1时为例），特征：随着x的变大，y值急速变大，即日常提到的指数级增长

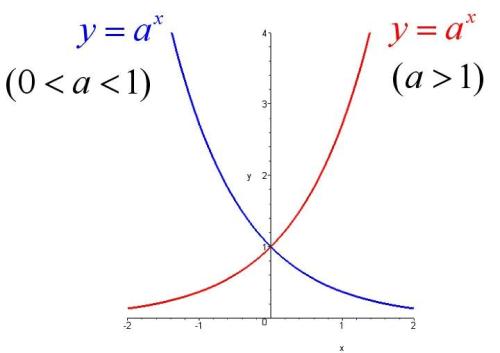
照进现实

对y的影响边际递增，若你的指标形态近似一条直线，而该指标对你的目标的影响应是边际递增的，那么，可以对该指标做对数，用作建模。常适用于比较低频业务的指标，该行为每发生一次，对我分析目标有重大影响。举例：某游戏的用户价值衡量，支付是低频行为，每支付一次对用户价值的贡献度较高，那么可对支付次数指标取对数，用于建模。

• 幂函数

公式如图：x是你的指标，用几次方取决于指标与目标的关系可视化形态

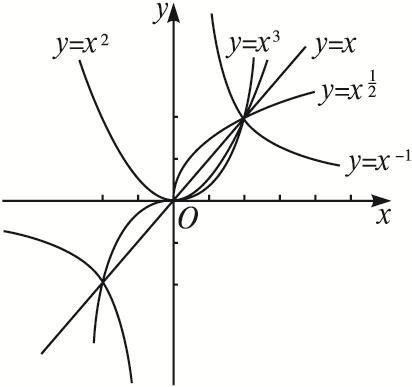
照进现实

与对数函数和指数函数的例子类似，想清楚你的业务，根据需要转换指标。

• -1次方即取你指标的倒数，指标越大，对目标的影响越小，反映的是负面影响；
• 取指标的负数也是指标越大对目标的影响越小，同样是反映负面影响，取用哪一个，取决于该指标对目标的影响是负的，还是多有正影响，只是越大影响越小。
• 1/2次数即取你指标的开根号，如图形态，接近对数函数，但边际贡献略大于指数函数，用哪个，取决于对你指标的判断。

Tips：使用时可以多个组合，不局限于一种，比如：取对数后再连乘。

其他数据转换的小tips

• 组合指标

1.矛盾的指标，组合处理

举例1：新增与留存，新增越大，留存越小，仅用留存用户数反映不了新增的留存质量，仅用留存率反映不了该渠道的大小，组合方式比如--ln(新增）*留存，即线对新增做函数转换，再与留存组合，将新增作为留存的权重处理。

2.相似的指标，组合处理

举例2：发帖数与发帖人数，两个指标衡量发帖活跃，可做组合处理，比如--ln(新增）*人均发帖数，真正反映用户活跃的人均可能更合适，但须将人数规模考虑进来。

• 剔除量纲（即剔除指标间自带的大小的差异，使指标间可比）
• 常见标准化方法：z-score方法；Max-min方法。对指标本身做标准化，剔除量纲的影响。
• 变异系数是标准差与平均数的比值，本质是将标准差进行标准化，使不同维护或指标的方差间存在可比性。
• 均值的其他玩法。使用均值剔除量纲影响，可以将首个指标作为基准，其他指标均以avg(首个指标)/avg(第i个指标）作为权重。

等等其他。掌握这样的思维，运用自己掌握的数学知识，去构建业务应有的数据形态，建模准确度会大大提高。

不论是数学建模还是机器学习，与业务紧密结合是基础要求，可以将模型认为合理的结果与业务探讨，请他们标注准确率，找到模型需要调整的方向，与业务多次往来，才会提升模型的可应用性。