机器学习：理解逻辑回归及二分类、多分类代码实践

数据分析学习社
数据分析学习社
数据分析学习社
348
文章
0
评论
更多
 2021-07-0310:10:42 评论 1,103 5443字
摘要

本文的概念相对简单，主要侧重于代码实践。现实生活中不止有预测的问题还有分类的问题。我们可以从预测值的类型上简单区分：连续变量的预测为回归，离散变量的预测为分类

机器学习：理解逻辑回归及二分类、多分类代码实践

逻辑回归：二分类

 

1.1 理解逻辑回归

我们把连续的预测值进行人工定义，边界的一边定义为 1，另一边定义为 0。这样我们就把回归问题转换成了分类问题。
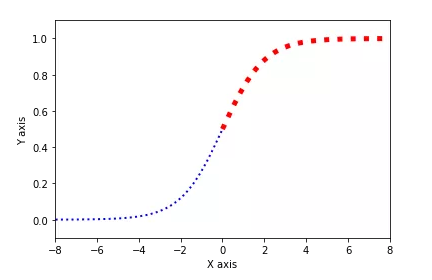
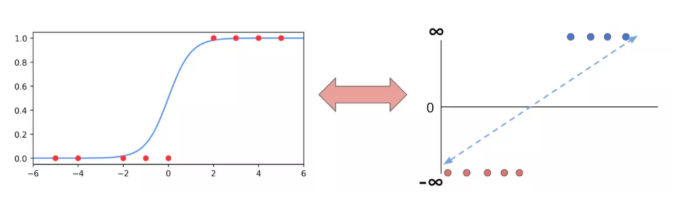
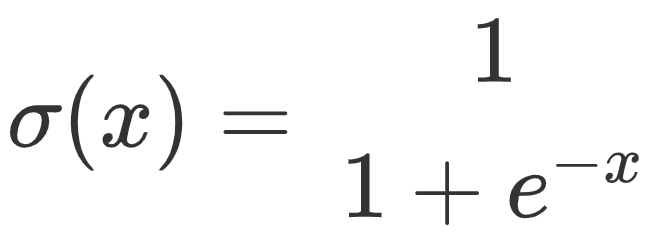
机器学习：理解逻辑回归及二分类、多分类代码实践
如上图，我们把连续的变量分布压制在 0-1 的范围内，并以 0.5 作为我们分类决策的边界，大于 0.5 的概率则判别为 1，小于 0.5 的概率则判别为 0。
机器学习：理解逻辑回归及二分类、多分类代码实践
我们无法使用无穷大和负无穷大进行算术运算，我们通过逻辑回归函数（Sigmoid 函数/S 型函数/Logistic 函数）可以讲数值计算限定在 0-1 之间。
机器学习：理解逻辑回归及二分类、多分类代码实践
以上就是逻辑回归的简单解释。下面我们应用真实的数据案例来进行二分类代码实践。

1.2 代码实践 - 导入数据集

添加引用：
  •  
  •  
  •  
  •  
import numpy as npimport pandas as pdimport seaborn as snsimport matplotlib.pyplot as plt
导入数据集（大家不用在意这个域名）：
  •  
  •  
df = pd.read_csv("https://blog.caiyongji.com/assets/hearing_test.csv")df.head()
age physical_score test_result
33
40.7
1
50
37.2
1
52
24.7
0
56
31
0
35
42.9
1
该数据集，对 5000 名参与者进行了一项实验，以研究年龄和身体健康对听力损失的影响，尤其是听高音的能力。此数据显示了研究结果对参与者进行了身体能力的评估和评分，然后必须进行音频测试（通过/不通过），以评估他们听到高频的能力。
  • 特征：1. 年龄 2. 健康得分
  • 标签：（1通过/0不通过）

1.3 观察数据

  •  
sns.scatterplot(x="age",y="physical_score",data=df,hue="test_result")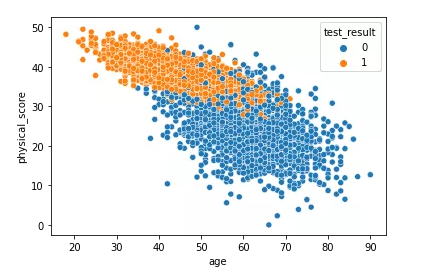
我们用 seaborn 绘制年龄和健康得分特征对应测试结果的散点图。
机器学习：理解逻辑回归及二分类、多分类代码实践
  •  
sns.pairplot(df,hue="test_result")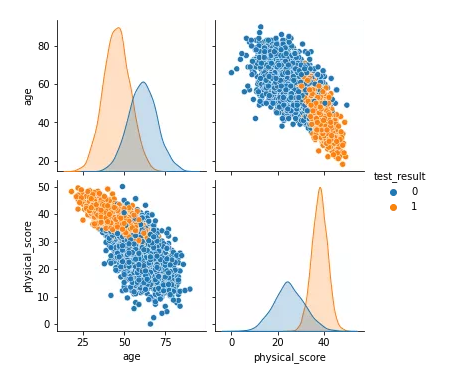
我们通过 pairplot 方法绘制特征两两之间的对应关系。
机器学习：理解逻辑回归及二分类、多分类代码实践
我们可以大致做出判断，当年龄超过 60 很难通过测试，通过测试者普遍健康得分超过 30。

1.4 训练模型

  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
from sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScalerfrom sklearn.linear_model import LogisticRegressionfrom sklearn.metrics import accuracy_score,classification_report,plot_confusion_matrix#准备数据X = df.drop("test_result",axis=1)y = df["test_result"]X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=50)scaler = StandardScaler()scaled_X_train = scaler.fit_transform(X_train)scaled_X_test = scaler.transform(X_test)#定义模型log_model = LogisticRegression()#训练模型log_model.fit(scaled_X_train,y_train)#预测数据y_pred = log_model.predict(scaled_X_test)accuracy_score(y_test,y_pred)
我们经过准备数据，定义模型为 LogisticRegression 逻辑回归模型，通过 fit 方法拟合训练数据，最后通过 predict 方法进行预测。最终我们调用 accuracy_score 方法得到模型的准确率为 92.2%。

 

机器学习：理解逻辑回归及二分类、多分类代码实践

模型性能评估：准确率、精确度、召回率

 

我们是如何得到准确率是 92.2%的呢？我们调用 plot_confusion_matrix 方法绘制混淆矩阵。
  •  
plot_confusion_matrix(log_model,scaled_X_test,y_test)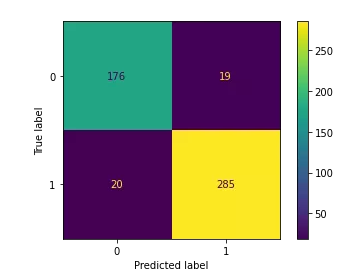
我们观察 500 个测试实例，得到矩阵如下：
机器学习：理解逻辑回归及二分类、多分类代码实践
我们对以上矩阵进行定义如下：
  • 真正类TP(True Positive) ：预测为正，实际结果为正。如，上图右下角285。
  • 真负类TN(True Negative) ：预测为负，实际结果为负。如，上图左上角176。
  • 假正类FP(False Positive) ：预测为正，实际结果为负。如，上图左下角19。
  • 假负类FN(False Negative) ：预测为负，实际结果为正。如，上图右上角20。
准确率(Accuracy) 公式如下：
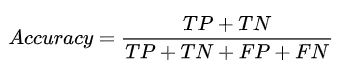
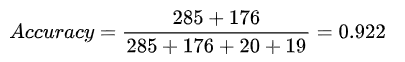
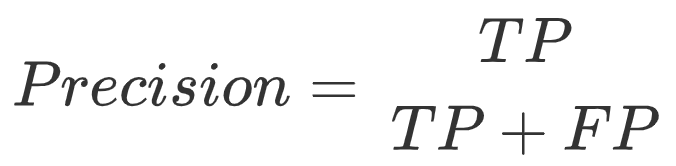
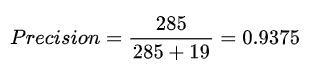
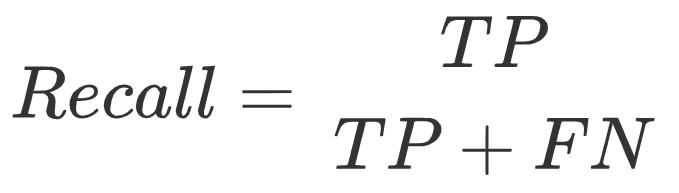
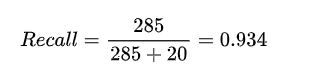
机器学习：理解逻辑回归及二分类、多分类代码实践
带入本例得：
机器学习：理解逻辑回归及二分类、多分类代码实践
精确度(Precision) 公式如下：
机器学习：理解逻辑回归及二分类、多分类代码实践
带入本例得：
机器学习：理解逻辑回归及二分类、多分类代码实践
召回率(Recall) 公式如下：
机器学习：理解逻辑回归及二分类、多分类代码实践
带入本例得：
机器学习：理解逻辑回归及二分类、多分类代码实践
我们调用 classification_report 方法可验证结果。
  •  
print(classification_report(y_test,y_pred))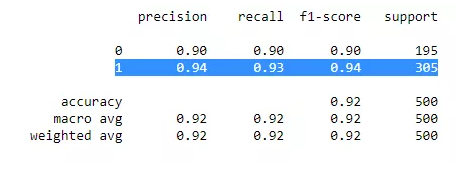
机器学习：理解逻辑回归及二分类、多分类代码实践

 

机器学习：理解逻辑回归及二分类、多分类代码实践

Softmax：多分类

 

3.1 理解 softmax 多元逻辑回归

Logistic 回归和 Softmax 回归都是基于线性回归的分类模型，两者无本质区别，都是从伯努利分结合最大对数似然估计。
最大似然估计：简单来说，最大似然估计就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值。
术语"概率"(probability)和"似然"(likelihood)在英语中经常互换使用，但是它们在统计学中的含义却大不相同。给定具有一些参数 θ 的统计模型，用"概率"一词描述未来的结果x的合理性（知道参数值 θ），而用"似然"一词表示描述在知道结果x之后，一组特定的参数值 θ 的合理性。
Softmax 回归模型首先计算出每个类的分数，然后对这些分数应用 softmax 函数，估计每个类的概率。我们预测具有最高估计概率的类，简单来说就是找得分最高的类。

3.2 代码实践 - 导入数据集

导入数据集（大家不用在意这个域名）：
  •  
  •  
df = pd.read_csv("https://blog.caiyongji.com/assets/iris.csv")df.head()
sepal_length sepal_width petal_length petal_width species
5.1
3.5
1.4
0.2
setosa
4.9
3
1.4
0.2
setosa
4.7
3.2
1.3
0.2
setosa
4.6
3.1
1.5
0.2
setosa
5
3.6
1.4
0.2
setosa
该数据集，包含 150 个鸢尾花样本数据，数据特征包含花瓣的长度和宽度和萼片的长度和宽度，包含三个属种的鸢尾花，分别是山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)。
  • 特征：1. 花萼长度 2. 花萼宽度 3. 花瓣长度 4 花萼宽度
  • 标签：种类：山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)

3.3 观察数据

 
  •  
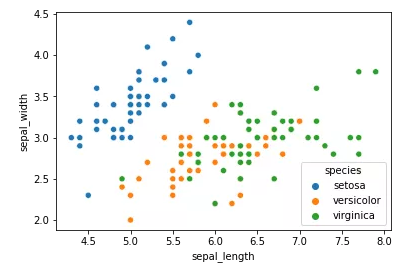
sns.scatterplot(x="sepal_length",y="sepal_width",data=df,hue="species")
我们用 seaborn 绘制花萼长度和宽度特征对应鸢尾花种类的散点图。
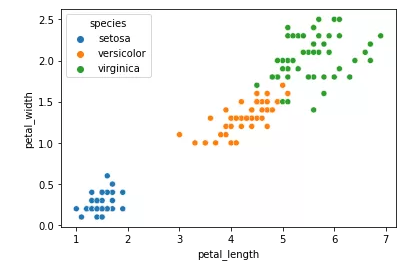
机器学习：理解逻辑回归及二分类、多分类代码实践
 
  •  
sns.scatterplot(x="petal_length",y="petal_width",data=df,hue="species")
我们用 seaborn 绘制花瓣长度和宽度特征对应鸢尾花种类的散点图。
机器学习：理解逻辑回归及二分类、多分类代码实践
  •  
sns.pairplot(df,hue="species")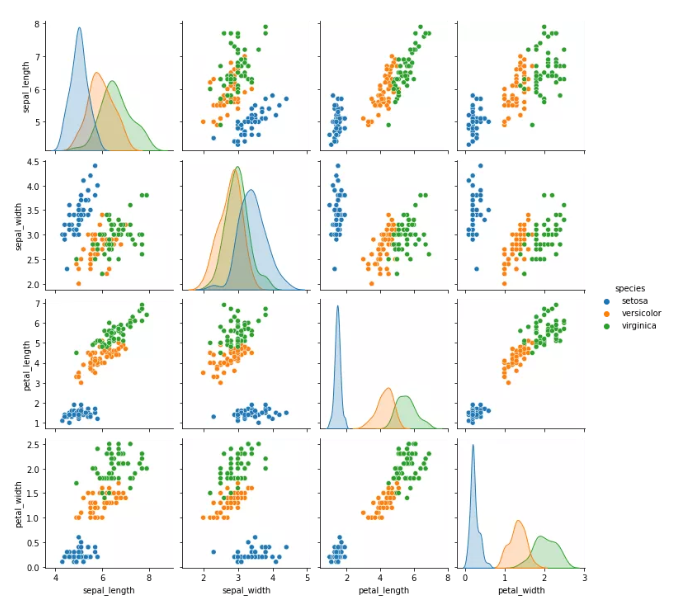
我们通过 pairplot 方法绘制特征两两之间的对应关系。
机器学习：理解逻辑回归及二分类、多分类代码实践
我们可以大致做出判断，综合考虑花瓣和花萼尺寸最小的为山鸢尾花，中等尺寸的为变色鸢尾花，尺寸最大的为维吉尼亚鸢尾花。

3.4 训练模型

  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
#准备数据X = df.drop("species",axis=1)y = df["species"]X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=50)scaler = StandardScaler()scaled_X_train = scaler.fit_transform(X_train)scaled_X_test = scaler.transform(X_test)#定义模型softmax_model = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=50)#训练模型softmax_model.fit(scaled_X_train,y_train)#预测数据y_pred = softmax_model.predict(scaled_X_test)accuracy_score(y_test,y_pred)
我们经过准备数据，定义模型 LogisticRegression 的 multi_class="multinomial"多元逻辑回归模型，设置求解器为 lbfgs，通过 fit 方法拟合训练数据，最后通过 predict 方法进行预测。最终我们调用 accuracy_score 方法得到模型的准确率为 92.1%。
我们调用 classification_report 方法查看准确率、精确度、召回率。
  •  
print(classification_report(y_test,y_pred))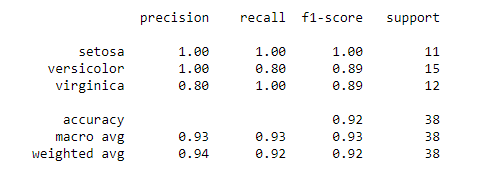
机器学习：理解逻辑回归及二分类、多分类代码实践

3.5 拓展：绘制花瓣分类

我们仅提取花瓣长度和花瓣宽度的特征来绘制鸢尾花的分类图像。
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
  •  
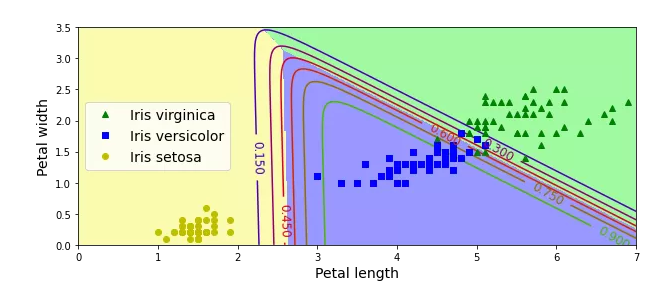
#提取特征X = df[["petal_length","petal_width"]].to_numpy() y = df["species"].factorize(["setosa", "versicolor","virginica"])[0]#定义模型softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=50)#训练模型softmax_reg.fit(X, y)#随机测试数据x0, x1 = np.meshgrid(        np.linspace(0, 8, 500).reshape(-1, 1),        np.linspace(0, 3.5, 200).reshape(-1, 1),    )X_new = np.c_[x0.ravel(), x1.ravel()]#预测y_proba = softmax_reg.predict_proba(X_new)y_predict = softmax_reg.predict(X_new)#绘制图像zz1 = y_proba[:, 1].reshape(x0.shape)zz = y_predict.reshape(x0.shape)plt.figure(figsize=(10, 4))plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")from matplotlib.colors import ListedColormapcustom_cmap = ListedColormap(["#fafab0","#9898ff","#a0faa0"])plt.contourf(x0, x1, zz, cmap=custom_cmap)contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)plt.clabel(contour, inline=1, fontsize=12)plt.xlabel("Petal length", fontsize=14)plt.ylabel("Petal width", fontsize=14)plt.legend(loc="center left", fontsize=14)plt.axis([0, 7, 0, 3.5])plt.show()
得到鸢尾花根据花瓣分类的图像如下：
机器学习：理解逻辑回归及二分类、多分类代码实践

 

机器学习：理解逻辑回归及二分类、多分类代码实践

小结

 

相比于概念的理解，本文更侧重上手实践，通过动手编程你应该有"手热"的感觉了。截至到本文，你应该对机器学习的概念有了一定的掌握，我们简单梳理一下：

  • 机器学习的分类

  • 机器学习的工业化流程

  • 特征、标签、实例、模型的概念

  • 过拟合、欠拟合

  • 损失函数、最小二乘法

  • 梯度下降、学习率

  • 线性回归、逻辑回归、多项式回归、逐步回归、岭回归、套索(Lasso)回归、弹性网络(ElasticNet)回归是最常用的回归技术

  • Sigmoid 函数、Softmax 函数、最大似然估计

 

 

End.

作者：caiyongji

本文为转载分享，如果涉及作品、版权和其他问题，请联系我们第一时间删除（微信号：lovedata0520）

更多文章前往首页浏览http://www.itongji.cn/

 

历史上的今天
7 月
3
  • 我的微信公众号
  • 微信扫一扫
  • weinxin
  • 我的微信公众号
  • 微信扫一扫
  • weinxin
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: