数据结构——图

前言

图是不同于前面两种数据结构的另一种新的数据结构，线性表中元素与元素之间是被串起来的，每个数据元素只有一个直接前驱和一个直接后继，是一种一对一的数据结构；在树的结构中，数据元素之间有明显的层次关系，并且每一层上的数据元素可能和下一层中多个元素相关，但只能和上一层中的一个元素相关，是一种一对多的数据结构举个例子就是你可以有多个孩子，但是只能有一对父母。但现实中的情况是，人与人之间的关系是复杂的，不是简单的线性关系，也不全是层级关系，而可能交叉相互关系，也就是多对多的数据情况，这就图的一个概念，图是一种多对多的数据结构。

图相关的各种定义

图：图是由结点的有穷集合V和边对的集合E组成，为了将图与树形结构进行区分，在图结构中常常将结点称为顶点，边是顶点的有序偶对。若两个顶点之间存在一条边，则表示这两个顶点具有相邻关系。

有向图和无向图：根据用来链接两个顶点之间的边是否有方向（箭头指向）分为有向图和无向图。

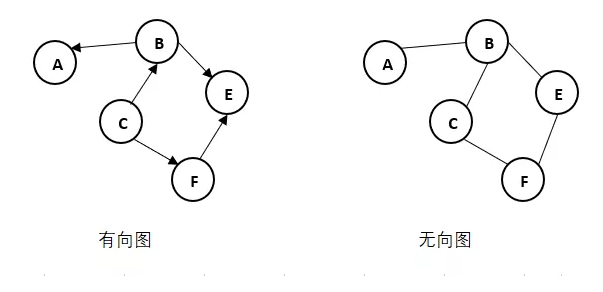
弧：在有向图中，通常将边称为弧，含箭头的一端称为弧端，另一端则称为弧尾，记作，表示从顶点vi到vj有一条边。

顶点的度、出度、入度：在无向图中，边记为（vi,vj），该式等价于有向图中的,两条边。与顶点v相关的边的条数称为顶点v的度。在有向图中指向顶点v的边的条数称为顶点v的入度，由顶点v发出的边的条数称为顶点v的出度。

有向完全图和无向完全图：若有向图中有n个顶点，则最多有n(n-1)条边（图中任意两个顶点都有两条边相连，且顶点A-B与顶点B-A是两条边），将具有n(n-1)条边的有向图称为有向完全图。若无向图中有n个顶点，则最多有n(n-1)/2条边（任意两个顶点之间都有一条边，且顶点A-B与顶点B-A是同一条边），将具有n(n-1)/2条边的无向图称为无向完全图。

路径和长度：在一个图中，路径为相邻顶点序偶所构成的序列。路径长度是指路径上边的数目。

简单路径：序列中顶点不重复出现的路径称为简单路径。

回路：若一条路径的第一个顶点和最后一个顶点相同，则这条路径是一条回路。

权和网：图中每条边都可以附带一个对应的数，这种与边相关的数称为权，权可以表示从一个顶点到另一个顶点的距离或者花费的代价。边上带有权的图称为带权图，也称为网。

图的存储结构

1.邻接矩阵

邻接矩阵是表示顶点之间相邻关系的矩阵。假设G=(V,E)是具有n个顶点的图，顶点序号依次为0，1，…，n-1,则G的邻接矩阵是具有如下定义的n阶方阵A：

A[i][j] = 1表示顶点i与j邻接，即i与j之间存在边或者弧。

A[i][j] = 0表示顶点i与j不邻接。

邻接矩阵是图的顺序存储结构，由邻接矩阵的行数或列数可知图中的顶点数。主要有三种图的邻接矩阵，有向图、无向图、有向有权图。

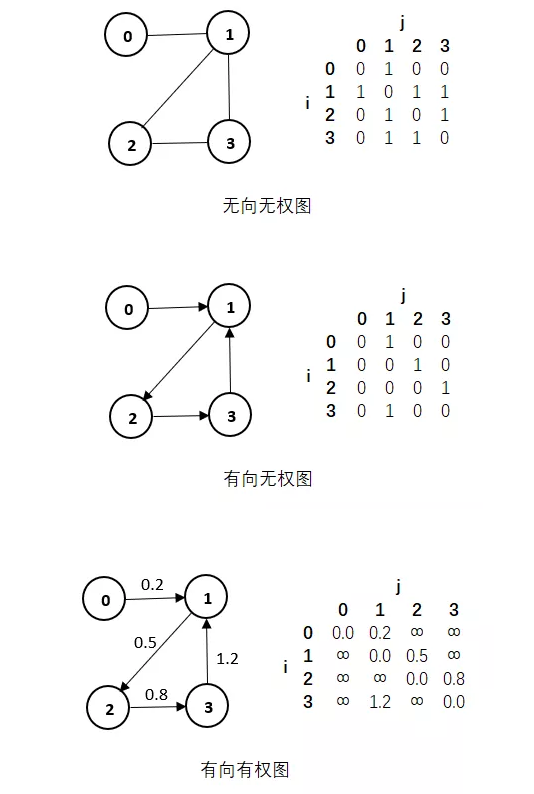
在无向无权图、有向有权图中，用0表示两顶点之间没有边的存在，用1表示两顶点之间有边的存在。

而在有向有权图中，顶点到顶点自身的距离为0，两顶点之间如果有边的存在，那么权值就是这两顶点之间的距离，如果两顶点之间没有边的存在，那么距离就是无穷大。

邻接矩阵的结构型定义：

typedef struct{    int no;    //顶点编号    char info;    //顶点其他信息}VertexType;    //顶点类型typedef struct    //图的定义{    int adges[maxsize][maxsize];    //邻接矩阵定义，如果是有权图，则需要将int变为float    int n,e;    //分别存放顶点数和边数    VertexType vex[maxsize];    //存放结点信息}MGraph;//图的邻接矩阵类型

2.邻接表

邻接表是图的一种链式存储结构，所谓邻接表就是对图中的每个顶点i建立一个单链表，每个单链表的第一个结点存放有关顶点的信息，把这一结点看作链表的表头，其余结点存放有关边的信息。

因此，邻接表由单链表的表头形成的顶点表和单链表的其余结点形成的边表两部分组成。一般顶点表存放顶点信息和指向第一个边结点指针，边表结点存放与当前顶点相邻接顶点的序号和指向下一个边结点指针。

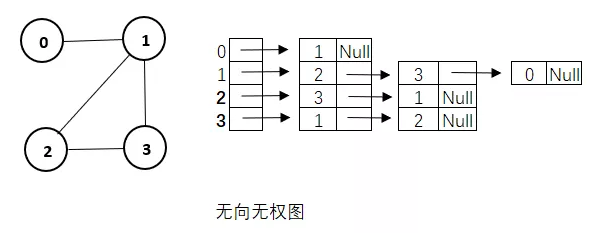
顶点0指向1，顶点1指向0、2、3，顶点2指向1、3，顶点3指向1、2。

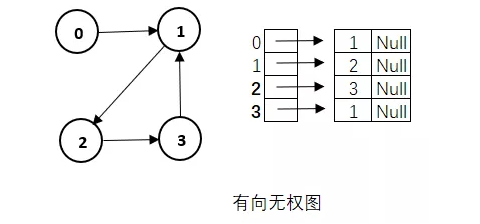
顶点0指向1权值为0.2，顶点1指向权值为0.5，顶点2指向3权值为0.8，顶点3指向1权值为1.2。

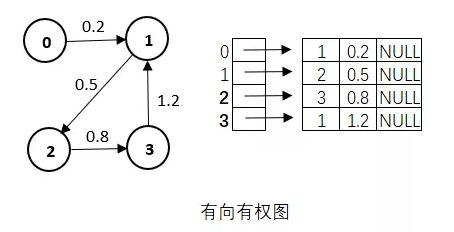
邻接表存储表示如下：

typedef struct ArcNode{    int adjvex;    //该边所指向的结点的位置    struct ArcNode *nextarc;    //指向下一条边的指针    int info;    //该边的其他附加信息，比如权值}ArcNode;typedef struct{    char data;    //顶点信息    ArcNode *firstarc;    //指向第一条边的指针}VNode;typedef struct{    VNode adjlist[maxsize];    //邻接表    int n,e;    //顶点数和边数}AGraph; 

图的遍历

1.深度优先搜索遍历(DFS)

顾名思义就是深度优先，也就是从一个顶点A出发，然后先遍历与顶点A相连接的顶点B，再遍历与顶点B连接的C，再遍历与C连接的D，直到没有与D连接的顶点，然后换一个顶点接着如此遍历。然后随机挑选一个未被遍历的顶点继续沿着边的方向进行遍历，直到所有顶点全部被访问。实现代码如下：

int visit[maxsize];    //visit[]是一个全局数组，用来记录哪些顶点已被访问，初始时，所有顶点全为0，表示未被访问，如果被访问，则将该顶点置为1void DFS(AGraph *G,int v){    ArcNode *p;        visit[v] = 1;    //遍历后就置为已访问    Visit(v);    //函数visit表示访问结点这个行为    p = G -> adjlist[v].firstarc;    //p指向顶点v的第一条边    while (p != NULL)    {        if(visit
 == 0)    //若顶点未访问，则递归访问它            DFS(G,p -> adjvex);            p = p -> nextarc;    //p指向顶点v的下一条边的终点    }}

2.广度优先搜索遍历(BFS)

顾名思义就是广度优先，先从顶点A出发，然后遍历所有与A连接的顶点B1、B2、B3、…、Bn，然后再依次遍历与顶点B1、B2、B3、…、Bn链接的所有顶点，同样，每遍历完一个顶点以后，标记为已遍历，直到所有的顶点都被遍历过为止。

广度优先遍历图的时候需要用到队列，遍历过程如下：

• 任取图中一个顶点访问，入队，并将这个点标记为已访问；
• 当队列不为空时循环执行：出队，依次检查出队顶点的所有邻接顶点，访问没有被访问过的邻接顶点并将其入队；
• 当队列为空时，跳出循环，遍历结束。

void BFS(AGraph *G,int V,int Visit[maxSize])    //visit[]数组被初始化为全0{    ArcNode *p;    int que[maxSize],front = 0,rear = 0;    //队列定义    int j;    Visit(v);    //任意访问顶点v的函数    visit[v] = 1;    rear = (rear + 1)%maxSize;    //当前顶点v进队    que[rear] = v;    while(front != rear)    //队空时说明遍历完成    {        front = （front+1）% maxsize;    //顶点出队        j = que[front];        p = G -> adjlist[j].firstarc;    //p指向出队顶点j的第一条边        while(p != NULL)    //当p的所有邻接点中未被访问的点入队        {            if(visit
 == 0)    //当前邻接顶点未被访问，则进队            {                Visit(p -> adjvex);                visit
 = 1;                rear = (rear+1)%maxSize;    //该顶点进队                que[rear] = p -> adjvex;            }        }    p = p -> nextarc;    //p指向j的下一条边    }}

End.爱数据网专栏作者：张俊红作者介绍：一个数据科学路上的学习者、实践者、传播者个人公众号：俊红的数据分析之路